- Outeur Matthew Elmers elmers@military-review.com.
- Public 2024-01-11 04:41.
- Laas verander 2025-01-24 09:18.
In hierdie artikel sal ons probeer om die wapenrusting van die gewere van die Bayern-, Rivenge- en Pennsylvania -slagskepe te verstaan, asook die vergelykende kwaliteit van die Duitse, Amerikaanse en Britse wapenrusting. Dit is uiters moeilik om dit te doen, want die data oor die Amerikaanse 356 mm, Duitse 380 mm en Britse 381 mm kanonne is baie sketsagtig en onvolledig en weerspreek mekaar soms, maar ons sal in elk geval probeer.
Wat presies is die probleem? Kom ons kyk hoe die meeste aanhangers van die vlootgeskiedenis (en nie net nie) die wapendringing van sekere wapens vergelyk. Byvoorbeeld: in een publikasie wat byvoorbeeld aan Engelse dreadnoughts gewy is, is daar inligting dat 'n Britse 381 mm-projektiel van die Eerste Wêreldoorlog 'n 381 mm-pantserplaat op 'n afstand van ongeveer 70 kabels deurboor het. In 'n ander uitgawe, gewy aan die reeds Duitse "hoofstad" skepe - dat 'n soortgelyke Duitse 380 mm -projektiel 350 mm pantser "bemeester" het met slegs 67,5 kabels. Dit blyk hieruit te volg dat die Engelse kanon kragtiger is - dit is presies die gevolgtrekking.
In werklikheid is dit egter baie maklik om sulke inligting op hierdie manier te vergelyk.
Word die bogenoemde gegewens verkry as gevolg van die werklike skietery, of word dit bereken met behulp van wapendringingstegnieke? As dit die resultate van die werklike skietery was, was die toestande dan dieselfde vir albei gewere? As die pantserpenetrasie deur berekening verkry is, is dieselfde metodes dan gebruik? Is die verkrygde data die resultaat van die werk van spesialiste van die betrokke ministeries en departemente, of is dit die resultaat van berekeninge deur historici wat 'n sakrekenaar opgeneem het? Dit is duidelik dat die akkuraatheid in die tweede geval baie laer sal wees … U hoef nie ver te gaan vir voorbeelde nie: kom ons neem die beroemde monografie van S. Vinogradov, "Superdreadnoughts of the Second Reich" Bayern "en" Baden ". In aanhangsel nr. 2 het die gerespekteerde historikus saam met V. L. Kofman maak 'n groot hoeveelheid berekeninge om die vermoëns van die slagskepe Rivenge en Bayern te vergelyk. Maar helaas, dit is genoeg om na die tabel met parameters vir 15-duim-gewere te kyk (p. 124) en ons sal sien dat, volgens die berekeninge van gerespekteerde skrywers, 'n Engelse 381-mm-geweer met 'n hoogtehoek van 20, 25 grade het 'n reikwydte van slegs 105 kabels, dit wil sê ongeveer 19, 5 duisend m. Terwyl vreemde bronne vir dieselfde aanvanklike snelheid (732 m / s) en 'n effens laer hoogtehoek (20 grade) aansienlik groter afstande gee - 21, 3-21, 7 duisend m. Natuurlik het sulke afwykings van reële waardes egter die negatiefste uitwerking op die berekeningresultate.
Maar selfs al gee die bronne die resultate van berekeninge van spesialiste aan, waarvan die akkuraatheid geen twyfel bestaan nie, kom 'n ander faktor wat die vergelyking bemoeilik: die punt hier is die kwaliteit van die wapenrusting. Dit is duidelik dat dieselfde Britte, by die berekening van pantserpenetrasie by die ontwerp van 'n spesifieke dreadnought, die ooreenstemmende aanwysers van Britse pantser, die Duitsers - onderskeidelik Duits, ens. En die wapenrusting van verskillende lande kan verskil in duursaamheid, maar dit is steeds die helfte van die moeilikheid: in dieselfde land is dieselfde Krupp -pantser voortdurend verbeter. Dit blyk dus dat die berekeninge van artilleriestelsels wat byvoorbeeld in Engeland gemaak is, en blykbaar vir dieselfde Krupp -wapenrusting, maar op verskillende tye gemaak is, onvergelykbaar kan blyk te wees. En as ons hierby die byna volledige afwesigheid van ernstige werk aan die evolusie van die pantserkas in verskillende lande ter wêreld byvoeg …
Oor die algemeen is 'n min of meer betroubare vergelyking van pantserpenetrasie nie so 'n eenvoudige taak as wat dit met die eerste oogopslag lyk nie. En op 'n vriendskaplike manier is dit beter dat 'n leek (wat sonder twyfel die skrywer van hierdie artikel is) hierdie saak nie aanpak nie. Maar helaas - tot ons diep spyt, is die voordele op een of ander manier nie haastig om hierdie kwessies te hanteer nie, so … soos hulle sê, in die afwesigheid van gestempelde papier, skryf ons in gewone teks.
Dit is natuurlik nie meer moontlik om op groot skaal toetse van bogenoemde artilleriestelsels uit te voer nie, dus is ons lot berekenings. En as dit die geval is, dan is dit nodig om ten minste 'n paar woorde te sê oor die wapenspenetrasieformules. As moderne berekeningsmetodes gepubliseer word, word die Jacob de Marr -formule gewoonlik slegs in geslote uitgawes en in populêre literatuur gegee. Dit is interessant dat professor van die Naval Academy L. G. Goncharov, in sy artilleriehandboek uit 1932, noem dit die Jacob de Marr -formule. Hierdie formule, saam met baie ander, was wydverspreid aan die begin van die vorige eeu, en ek moet sê dat dit baie akkuraat is - miskien is dit selfs die akkuraatste onder soortgelyke formules van daardie jare.
Die eienaardigheid daarvan is dat dit nie fisies is nie, dit wil sê, dit is nie 'n wiskundige beskrywing van fisiese prosesse nie. De Marr se formule is empiries, dit weerspieël die resultate van eksperimentele beskutting van yster en staal-yster harnas. Ten spyte van hierdie 'onwetenskaplike aard', het de Marr se formule 'n beter benadering getoon tot die werklike resultate van skietery en op Krupp -pantser as ander algemene formules, en daarom sal ons dit vir berekeninge gebruik.
Belangstellendes vind hierdie formule in die aanhangsel van hierdie artikel, maar dit is nie nodig om almal wat hierdie materiaal lees, te dwing om dit te verstaan nie - dit is nie nodig om die gevolgtrekkings van die artikel te verstaan nie. Ons neem slegs kennis dat die berekening baie eenvoudige en bekende konsepte gebruik vir almal wat belangstel in die geskiedenis van militêre vloot. Dit is die massa en kaliber van die projektiel, die dikte van die wapenrusting, die hoek waarteen die projektiel die wapenrusting tref, sowel as die snelheid van die projektiel wanneer dit die wapenrustingsplaat tref. De Marr kon hom natuurlik egter nie tot die bogenoemde parameters beperk nie. Die penetrasie van 'n projektiel hang immers nie net af van die kaliber en massa nie, maar ook tot 'n sekere mate van die vorm en die kwaliteit van die staal waaruit dit gemaak is. En die dikte van die pantserplaat, wat die projektiel kan oorkom, hang natuurlik nie alleen af van die prestasie van die projektiel nie, maar ook van die kwaliteit van die pantser. Daarom het de Marr 'n spesiale koëffisiënt in die formule ingebring, wat eintlik ontwerp is om die aangeduide kwaliteite van pantser en 'n projektiel in ag te neem. Hierdie koëffisiënt styg met 'n toename in die wapenrusting en neem af met 'n agteruitgang in die vorm en kwaliteit van die projektiel.
Die grootste probleem om die artilleriestelsels van verskillende lande te vergelyk, is eintlik 'berus' op hierdie koëffisiënt, wat ons in die toekoms eenvoudig sal noem (K). Ons sal dit vir elk van die bogenoemde gereedskap moet vind - as ons natuurlik 'n ietwat korrekte resultaat wil kry.
Laat ons dus eers redelik wydverspreide gegewens neem oor die pantserpenetrasie van die Duitse 380 mm / 45-geweer "Bayern", waarvolgens die geweer op 'n afstand van 12 500 m (dieselfde 67, 5 kabels) 350 mm kan deurdring wapenrusting. Ons gebruik 'n ballistiese sakrekenaar om die parameters van 'n projektiel van 750 kg op te spoor, met 'n aanvanklike snelheid van 800 m / s op die oomblik van impak op die wapenrusting: dit blyk dat so 'n projektiel 'n streng vertikaal geplaasde pantserplaat teen 'n hoek van 10, 39 grade, met 'n spoed van 505, 8 m / sek. 'N Klein vrywaring - hierna, as ons praat oor die invalshoek van die projektiel, bedoel ons die sogenaamde "hoek van die normale". 'Normaal' is wanneer die projektiel die hoekplaat streng loodreg op die oppervlak daarvan, dit wil sê teen 'n hoek van 90 grade, tref. Gevolglik het die projektiel teen 'n hoek van 10 grade getref.van die normale af beteken dat dit die plaat teen 'n hoek van 80 grade getref het. na die oppervlak, afwykend van die "verwysing" 90 grade. met 10 grade.
Maar terug na die pantserpenetrasie van die Duitse geweer. Die koëffisiënt (K) sal in hierdie geval ongeveer (afgerond tot die naaste heelgetal) gelyk wees aan 2,083 - hierdie waarde moet as normaal beskou word vir die wapenrusting van die era van die Eerste Wêreldoorlog. Maar hier ontstaan 'n probleem: die bron van gegewens oor pantserpenetrasie is die boek "German Capital Ships of World War Two", waar die 380 mm / 45-geweer van die Bayern vergelyk is met die hoofkaliber van die slagskip "Bismarck". En kan dit nie wees dat die berekening die aanwysers van die Krupp -wapenrusting in ag geneem het wat in die interval tussen die twee wêreldoorloë ontstaan het, wat baie sterker was as die wat op die Bayenne, Rivenge en Pennsylvania geïnstalleer is nie? Boonop berig die elektroniese ensiklopedie navweaps dat daar bewyse is dat op 'n afstand van 20 000 m Duitse 380 mm-skulpe 336 mm-pantserplaat kon binnedring, en ons praat van wapens van die era van die Eerste Wêreldoorlog.
Wel, ons glo: op 20 km sal die invalshoek 23,9 grade wees, die snelheid van die projektiel op die pantser is 410,9 m / s, en die koëffisiënt (K) - 'n paar ongelukkige 1618, wat nie in die pantser pas nie weerstandswaardes op alle tye van die Eerste Wêreldoorlog. 'N Soortgelyke resultaat bring oor die algemeen Duits-vervaardigde Krupp-pantser nader aan homogene pantserweerstand … Uiteraard bevat die navweaps-data 'n soort fout.
Kom ons probeer dan om 'n ander inligtingsbron te gebruik. Tot dusver het ons die berekende data gebruik, en nou sal ons probeer om dit te vergelyk met die resultate van die werklike toetse van die Duitse 380 mm / 45 kanon: dié word deur S. Vinogradov gegee in die bogenoemde monografie gewy aan Duits slagskepe.
Dit beskryf die gevolge van 3 skote met pantser-deurdringende projektiele, teen pantserplate met 'n dikte van 200, 290 en 450 mm, waarvan laasgenoemde die interessantste vir ons is: 'n projektiel wat 734 kg weeg, tref die pantserplaat in 'n hoek van 0 (dit wil sê op 90 grade na die oppervlak) en teen 'n snelheid van 551 m / s 450 mm deur die plaat geslaan. 'N Soortgelyke resultaat stem ooreen met die koëffisiënt (K) 1 913, maar dit sal in werklikheid effens laer wees, omdat die Duitsers hul projektiel tot 2 530 m agter die hindernis gevind het, en - in die algemeen. Helaas, omdat ek geen gegewens het oor hoeveel van hierdie afstand die projektiel deur die lug gevlieg het nie, hoeveel "op die grond" gery het, is dit absoluut onmoontlik om die energie te bepaal wat daardeur gestoor word na pantserpenetrasie.
Kom ons neem nou die Britse 381 mm / 42 artilleriestelsel. Helaas, die gegewens oor die pantserpenetrasie daarvan is nogal vaag: byvoorbeeld, V. L. Kofman, daar word melding gemaak van die feit dat hierdie Britse gewere deur pantser, die dikte van hul eie kaliber, op 'n afstand van ongeveer 70 kabels deurboor is. Maar met watter projektiel en met watter aanvanklike snelheid? Met inagneming van die feit dat die verwysing vervat is in die monografie wat gewy is aan die strydkruiser "Hood", en verwys na die tydperk van die skepping van hierdie skip, kan aanvaar word dat ons praat van 'n dop van 871 kg. 'N Ander vraag ontstaan egter hier: die amptelike aanvangsnelheid van so 'n projektiel was 752 m / s, maar sommige berekenings van die Britte is teen 'n laer spoed van 732 m / s uitgevoer, so watter waarde moet ons neem? Wat ook al van die aangeduide snelhede ons neem, die koëffisiënt (K) sal wissel binne 1 983 - 2 048, en dit is hoër as wat ons bereken het vir die waarde (K) vir die Duitse geweer. Daar kan aanvaar word dat dit spreek van die superioriteit van die kwaliteit van die Britse pantser in vergelyking met die Duitse … of is dit dat die geometriese vorm van die Duitse projektiel beter geskik was vir deurdringende pantsers? Of miskien is die hele punt dat die data van V. L. Kofman is berekende waardes, maar sou die Britse skulpe in die praktyk 'n beter resultaat behaal?
Wel, ons beskik oor data oor die resultate van die beskieting van die slagskip "Baden"

Dus, een van die Britse skulpe wat teen 'n hoek van 18 grade slaan. teen 'n snelheid van 472 m / sek., het die 350 mm voorste pantser van die Duitse hoofkaliber-rewolwer "oorweldig". Hierdie gegewens is des te waardevoller, want in hierdie geval is nie die Britse, maar die Duitse wapenrusting aan beskietings blootgestel, dit wil sê die toetse van 381 mm / 42 en 380 mm / 45 gewere is dus in 'n enkele koördinaatstelsel.
Helaas, hulle help ons nie te veel nie. As ons aanneem dat die Engelse dop die Duitse toring deurboor het, soos hulle sê, "met die laaste bietjie krag", en as daar 351 mm pantser was, sou dit misluk het, dan sou sy (K) gelyk wees aan 2 021. Dit interessant, terloops, dat S. Vinogradov verklaar dat die Britse projektiel, wat die 350 mm voorste pantser van die Duitse toring binnegedring het, nie later gevind is nie, maar in werklikheid lui die verslag iets anders - dit het ontplof en daar is 'n beskrywing van waar die fragmente in die toring gevlieg het.
Ons het natuurlik geen absolute gronde om aan te neem dat hierdie penetrasie die limiet was vir 'n 381 mm-projektiel, of selfs naby dit nie. Maar volgens sommige indirekte tekens kan dit aanvaar word dat dit presies die geval was. 'N Ander treffer gee 'n aanduiding hiervan: 'n Britse projektiel van 871 kg wat 'n hak van 350 mm teen 'n hoek van 11 grade tref, alhoewel dit 'n gat in die pantser met 'n deursnee van 40 cm kon maak, het dit nie binne -in die barbet gekom nie self, bars in die proses om die wapenrusting te oorkom. In hierdie geval het die treffer amper in die middel van die barbet plaasgevind, dit wil sê die kromming van die pantserplaat, as dit 'n invloed gehad het, was dit die minimum.
Uit al die bogenoemde kan 'n mens 'n paar gevolgtrekkings probeer maak, maar as gevolg van die broosheid van die bewysbasis, sal dit natuurlik baie veronderstel wees.
Gevolgtrekking 1: Duitse wapenrusting tydens die Eerste Wêreldoorlog het ongeveer die Britte ooreenstem met betrekking tot duursaamheid. Hierdie gevolgtrekking is geldig indien die verklaring van V. L. Kofman dat die Britse 381 mm / 42 geweer in staat was om wapens gelyk aan sy kaliber met 70 kbt deur te dring, en as ons ons nie vergis in die veronderstelling dat die penetrasie van 350 mm van die frontplaat van die Duitse rewolwer teen 'n hoek van 18 grade en 'n spoed van 472 m / s … is die grens of baie naby aan die penetrasiegrens van die Britse 381 mm -projektiel.
Gevolgtrekking 2de. Die vorm en kwaliteit van die Duitse 380 mm-projektiel het blykbaar 'n beter pantserpenetrasie gebied as die Engelse. Op grond van die bogenoemde gegewens, kan ons aanneem dat die koëffisiënt (K) van die Britse 381 mm -projektiel by die vuur op die Duitse pantser ongeveer 2 000 was, terwyl die Duitse 380 mm -projektiel ongeveer 1 900 was. As ons eerste korrek is, is die gevolgtrekking dat wapenweerstand van die Britse en Duitse wapenrusting is ongeveer gelyk, dit is duidelik dat die enigste rede vir die laer koëffisiënt (K) slegs die projektiel self kan wees.
Waarom kan 'n Duitse dop beter wees? Die kaliber is effens kleiner, met 'n millimeter, maar dit kan natuurlik nie 'n beduidende uitwerking hê nie. Die berekening toon dat met dieselfde massa (750 kg), 'n verandering in kaliber met 1 millimeter sal lei tot 'n toename in pantserpenetrasie met 1,03 millimeter. Die Duitse projektiel is ook korter - sy lengte was 3,5 kaliber, terwyl die lengte van die Britse "Greenboy" 4 kaliber is. Daar was moontlik ook ander verskille. Natuurlik speel die kwaliteit van die staal waaruit die projektiel gemaak word 'n belangrike rol.
Kom ons bereken nou die pantserpenetrasie van die Duitse en Britse gewere vir 'n afstand van 75 kabels - 'n algemeen aanvaarde afstand vir 'n beslissende geveg, waar 'n mens genoeg treffers kan verwag om 'n vyandelike skip van die lyn te vernietig.
Op die aangeduide afstand het 871 kg van 'n Britse 381 mm / 42 kanonskulp, wat met 'n aanvanklike snelheid van 752 m / s afgevuur is, die vertikaal geplaasde pantserplaat teen 'n hoek van 13,05 grade getref en die snelheid daarvan "op die bord" was 479,6 m / s … Met (K) gelyk aan 2,000, volgens die formule van Jacob de Marr, was die pantserpenetrasie van die Britse projektiel 376,2 mm.
Wat die Duitse dop betref, is alles 'n bietjie ingewikkelder. As ons tot die gevolgtrekking gekom het dat dit die Engelse oortref in terme van pantserpenetrasie, korrek is, dan was die vermoëns van die Duitse 380 mm / 45-geweer op 75 kabels baie naby aan die Engelse vyftien-duim-geweer. Op hierdie afstand het die Duitse projektiel van 750 kg die teiken teen 'n hoek van 12,42 grade teen 'n snelheid van 482,2 m / s getref, en by (K) gelyk aan 1 900 was die pantserpenetrasie 368,9 mm. Maar as die skrywer van hierdie artikel nog steeds 'n fout maak, en vir die Duitse geweer is dit die moeite werd om dieselfde koëffisiënt as die Engelse geweer te gebruik, dan val die vermoëns van die 380 mm-projektiel tot 342,9 mm.
Volgens die skrywer is die pantserpenetrasie van die Duitse projektiel egter die naaste aan 368, 9 mm (praktiese vuur het immers 'n koëffisiënt van 1 913 opgelewer, ondanks die feit dat die projektiel toe 2,5 km gevlieg het), maar die pantserpenetrasie van die Engelse projektiel kan effens laer bereken word. Oor die algemeen kan daar aanvaar word dat die Britse en Duitse artilleriestelsels op 'n afstand van 75 kabels redelik vergelykbaar is ten opsigte van pantserdringing.
Maar met die Amerikaanse 356 mm / 45 -geweer het alles baie interessanter geword. Die data wat voorheen aangehaal is vir skulpe wat 680 kg weeg, moet in die Russies-taalkundige literatuur as kanonies beskou word.
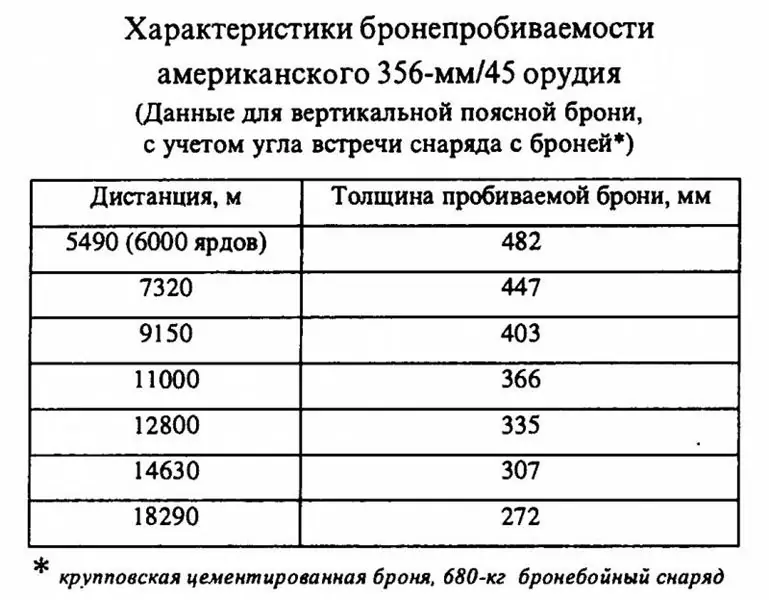
In werklikheid blyk dit dat die waardes wat daarin aangedui word, tot heeltemal voor die hand liggende gevolgtrekkings lei: as selfs die skulpe van 680 kg wat in 1923 in die Verenigde State verskyn het, minderwaardig is ten spyte van hul 380-381 mm Europese " kollegas ", dan wat werklik praat van die vroeëre skulpe van 635 kg, wat toegerus was met 356 mm artillerie Amerikaanse dreadnoughts! Hulle is ligter, wat beteken dat hulle vinniger spoed verloor tydens vlug, terwyl hul aanvanklike spoed nie swaarder doppe oorskry het nie, en wat vorm en kwaliteit betref, behoort die ammunisie van 1923 'n voordeel te hê. Dit is so duidelik soos die dag dat die Amerikaanse "Pennsylvania" ten tyde van die inwerkingtreding minderwaardig was ten opsigte van wapenrusting deur die Britse en Duitse dreadnoughts. Wel, dit is duidelik, is dit nie?
Dit is presies die gevolgtrekking wat die skrywer gemaak het, in ag genome die vermoëns van Amerikaanse veertien duim kanonne in die artikel "Standard" slagskepe van die VSA, Duitsland en Engeland. Amerikaanse "Pennsylvania" ". En toe tel hy 'n sakrekenaar op …
Die feit is dat die berekening volgens die de Marra-formule getoon het dat die Amerikaanse 356 mm / 45 gewere die pantserdringing in die tabel aangedui het met 'n koëffisiënt (K) gelyk aan 2,317! Met ander woorde, die Amerikaanse projektiele van 680 kg wat in die tabel getoon word, het die resultate getoon toe dit blootgestel was aan wapens wat nie in die era van die Eerste Wêreldoorlog geskep is nie, maar op baie later en duursame monsters.
Dit is moeilik om te sê hoeveel die sterkte van wapenbeskerming toegeneem het tussen die eerste en tweede wêreldoorloë. In Russies-taalbronne is daar slegs kort en dikwels teenstrydige verwysings na hierdie kwessie, op grond waarvan aangeneem kan word dat die sterkte van Krupp se wapenrusting met ongeveer 20-25%toegeneem het. Vir grootskaalse skulpe uit die era van die Eerste Wêreld sal die koëffisiënt (K) van 1,900 - 2,000 tot 2,280 - 2,500 groei, maar hier moet onthou word dat met 'n toename in die kwaliteit van pantserbeskerming die kwaliteit van die skulpe het natuurlik ook toegeneem, en daarom kan swaar ammunisie van die Tweede Wêreldoorlog (K) minder wees. Daarom lyk (K) in die bedrag van 2,317 vir na-oorlogse skulpe, natuurlik verbeter met inagneming van die ervaring wat opgedoen is, redelik organies, maar vir die wapenrusting van die era van die Tweede Wêreldoorlog, nie die eerste nie.
Maar deur die koëffisiënt (K) vir die Amerikaanse skulpe van 680 kg op 2 000 te stel, dit wil sê deur die kwaliteit van wapenrustingsbeskerming na die era van die Eerste Wêreldoorlog te bring, kry ons 'n afstand van 75 kabels penetrasie op 'n vlak van 393,5 mm, dit wil sê, hoër as die van die Britse en Duitse vyftien duim gewere!

Omskakeling na 635 kg projektiel gee 'n baie onbeduidende regstelling - die ballistiese sakrekenaar het getoon dat op 'n afstand van 75 kabels, met 'n invalshoek van 10, 82 grade. en die snelheid "op die wapenrusting" 533, 2 m by (K) gelyk aan 2,000, dring die Amerikaanse projektiel deur die wapenrusting van die era van die Eerste Wêreldoorlog, 380 mm dik, dit wil sê aansienlik meer as sy eie kaliber!
Aan die ander kant is dit heel moontlik dat so 'n berekening steeds nie heeltemal korrek is nie. Die feit is dat, volgens sommige verslae, die koëffisiënt (K) vir dieselfde pantser afneem met 'n toename in die kaliber van die projektiel. In ons berekeninge, byvoorbeeld, is die maksimum waarde (K) vir die Duitse 380 mm / 45 artilleriestelsel, verkry deur berekening en in bronne gepubliseer, 2,083. Terselfdertyd is die berekeninge vir die Duitse 305 mm / 50 gewere wat op Kaiserlichmarine-skepe geïnstalleer is wat begin met die Helgolande, gee die gegewens van bronne oor pantserdringing (K) op 'n vlak van 2 145. Gevolglik is dit moontlik dat die 356 mm / 45 gewere (K) = 2 000 ons het geneem vir die berekening van die pantserpenetrasie van Amerikaanse gewere is nog steeds te klein.
Boonop het die skrywer ongelukkig geen 'leidrade' om die wapenrusting van die Amerikaanse Krupp -wapenrusting met sy Europese eweknieë te vergelyk nie. Daar is niks meer as om dit gelyk te stel aan die Duitse en Engelse wapenbeskerming nie, hoewel dit natuurlik nie die geval is nie.
Kom ons som al hierdie taamlik chaotiese gegewens op. Met inagneming van die foute van die "metodes" wat in die berekeninge gebruik word, kan met 'n hoë waarskynlikheid aanvaar word dat Die pantserpenetrasie van die vertikale pantserbeskerming van die hoofkalibergewere van die slagskepe Rivenge, Bayern en Pennsylvania op 'n afstand van 75 kabels was ongeveer dieselfde en was ongeveer 365-380 mm.
Ten spyte van 'n klomp aannames, stel die gegewens tot ons beskikking ons steeds in staat om 'n paar gevolgtrekkings te maak rakende vertikale wapenbeskerming. Maar met die deurbraak van horisontale versperrings, wat gepantserde dekke is, is alles baie ingewikkelder. Die feit is dat Jacob de Marr ongelukkig glad nie die moeite gedoen het om 'n formule te skep om die sterkte van die horisontale verdediging te bepaal nie. Die basiese formule, aangepas vir moderne wapens, is slegs geskik vir die berekening van gepantserde pantsers met 'n dikte van meer as 75 mm. Hierdie formule word in aanhangsel nr. 1 by hierdie artikel gegee, en al die vorige berekeninge in die artikel is met behulp daarvan gemaak.
Maar die dekke van skepe van daardie jare is nie beskerm deur gesementeerde (heterogene) nie, maar deur homogene pantser, wat nie 'n oppervlakverhardde laag gehad het nie. Vir so 'n pantser (maar - vertikaal geïnstalleer!) Word 'n ander formule gebruik, wat bedoel is vir die evaluering van nie -gesementeerde pantserplate met 'n dikte van minder as 75 mm, dit word in bylaag nr. 2 gegee.
Ek wil daarop let dat albei hierdie formules uit 'n meer as ernstige bron geneem is: 'The course of naval tactics. Artillerie en wapenrusting 1932, skrywer - professor van die RKKA Naval Academy L. G. Goncharov, een van die voorste kenners in die vooroorlogse USSR op die gebied van vlootartillerie.
En helaas, nie een van hulle is geskik vir die beoordeling van die duursaamheid van horisontale beskerming nie. As ons die formule vir gesementeerde wapenrusting gebruik, kry ons op 'n afstand van 75 kabels skaars pantserdringing: 46,6 mm vir 381 mm / 42 Britte, 39,5 mm vir 380 mm / 45 Duits en 33,8 mm vir 356 mm / 45 Amerikaanse gewere. As ons die tweede formule vir nie -gesementeerde wapenrusting gebruik, kry ons dat al drie artilleriestelsels maklik deur 'n 74 mm pantserplaat kan dring, waarna 'n groot voorraad kinetiese energie behoue bly -as dit tipies op 'n afstand van 75 kabels getref word - byvoorbeeld, die Engelse 381 mm, 'n projektiel om 'n pantser van hierdie dikte op 'n afstand van 75 kabels binne te dring, sal 'n snelheid van 264,5 m / s hê, terwyl die snelheid daarvan 482,2 m / s sal wees. As ons die beperking op die dikte van die pantserplaat ignoreer, blyk dit dat die Britse 381 mm-projektiel volgens bogenoemde formule in staat is om dekwapens met 'n dikte van meer as 180 mm te penetreer! Wat natuurlik heeltemal onmoontlik is.
As ons probeer om te verwys na die toetsuitslae van die slagskip van die Bayern-klas, sal ons sien dat die Britse doppels van 871 kg met pantser twee keer die horisontale wapenrusting van die torings getref het, met 'n dikte van 100 mm in 'n hoek van 11 grade, wat ooreenstem met 'n afstand van 67,5 kabels vir 'n projektiel met 'n aanvanklike snelheid van 752 m / s en 65 kabels - vir 'n projektiel met 'n aanvangsnelheid van 732 m / s. Beide kere is die wapenrusting nie deurboor nie. Maar in een geval het die projektiel, ricocheting, 'n groef in die pantser gemaak met 'n diepte van 70 cm, dit wil sê die plaat was baie sterk gebuig. En in die tweede, alhoewel die dop weer ricochet was, was die pantser nie net 10 cm konkaaf nie, maar ook geskeur.

Die soortgelyke aard van die skade dui daarop dat, alhoewel die Duitse 100 mm -wapenrusting op die aangeduide afstande beskerming gebied het, dit, indien nie aan die grens van die moontlike nie, dit baie naby was. Maar die berekening volgens die formule vir gepantserde wapenrusting gee 'n pantserpenetrasie van slegs 46,6 mm op 'n groter afstand, waar die invalshoek hoër sal wees, en gevolglik sou dit makliker wees vir die projektiel om die dekwapens binne te dring. Dit wil sê, volgens die formule blyk dit dat die 100 mm -dek skertsend en met 'n groot veiligheidsmarge Engelse skulpe moet weerspieël - maar die praktyk bevestig dit nie. Terselfdertyd blyk dit uit berekeninge volgens die formule vir nie -gesementeerde wapenrusting dat die dakke van die hoofkaliber van Baden maklik deurboor moes gewees het, en - met 'n groot hoeveelheid dop -energie - wat weer nie glad bevestig deur die praktyk.
Ek moet sê dat sulke onjuisthede in die berekeninge 'n heeltemal logiese verduideliking het. Soos ons vroeër gesê het, is die formules van De Marr nie 'n wiskundige beskrywing van fisiese prosesse nie, maar slegs 'n vasstelling van die patrone wat verkry word tydens die toets van wapens. Maar vertikale pantserbeskerming, nie horisontaal nie, is getoets, en dit is glad nie verbasend dat die patrone in hierdie geval eenvoudig ophou werk nie: vir horisontaal geleë pantsers waarin die skulpe teen 'n baie klein hoek na hul oppervlak raak, is natuurlik heeltemal anders.
Die skrywer van hierdie artikel het op die internet gedink dat die formules van De Marr effektief werk by afwykingshoeke van die normale nie meer as 60 grade nie, dit wil sê van 30 grade tot op die oppervlak van die plaat en meer. Daar kan aanvaar word dat hierdie beoordeling baie naby aan die waarheid is.
Ons moet dus met spyt verklaar dat die wiskundige apparaat wat die outeur beskikbaar het, nie betroubare berekeninge van die horisontale beskermingsweerstand van die gevegskepe Rivenge, Bayern en Pennsylvania moontlik maak nie. Met die oog op die voorafgaande, sal dit moeilik wees om die gegewens oor die pantserpenetrasie van die horisontale pantser wat in verskillende bronne gegee is, te gebruik - as 'n reël is dit almal gebaseer op dieselfde berekeninge volgens de Marr se formules en is dit verkeerd.






