- Outeur Matthew Elmers [email protected].
- Public 2023-12-16 21:50.
- Laas verander 2025-01-24 09:18.

Wat bepaal akkuraatheid - een van die belangrikste kenmerke van 'n wapen? Uiteraard, van die kwaliteit van die vat en die patroon. Laat ons die patroon vir eers uitstel, maar kyk na die fisika van die proses.
Neem 'n metaalstaaf of buis van elastiese metaal en maak dit stewig vas in 'n massiewe basis. Ons kry dus 'n model van die toestel wat bestudeer word. As ons nou die staaf tref, maak dit nie saak op watter plek en in watter rigting nie, óf trek dit terug, druk dit vas, of laastens, as u 'n patroon in die buis steek en 'n skoot afvuur, sal ons sien dat die staaf (vat) in 'n gedempte ossillasiebeweging gekom het. Hierdie trillings word in die eenvoudigste ontbind, en elke tipe van so 'n eenvoudige trilling van die loop sal die akkuraatheid (akkuraatheid) van die skiet op sy eie manier beïnvloed.
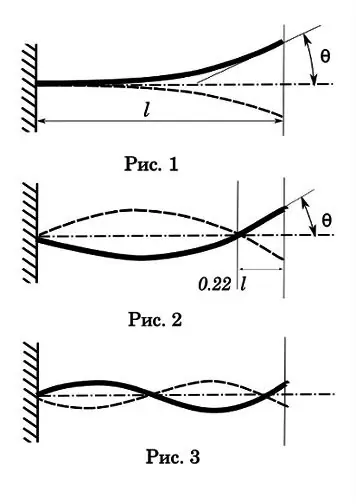
Kom ons begin met die eerste orde of toonhoogte vibrasies. Soos u kan sien (fig. 1), het so 'n ossillasie slegs een knoop by die aanhegtingspunt, die grootste amplitude, die langste vervalstyd en die langste ossillasietyd van een periode. Hierdie tyd is 0,017-0,033 sek. Die koeëlreistyd deur die boor is 0, 001-0, 002 sek. Dit wil sê, aansienlik minder as die siklus van een ossillasie, wat beteken dat hierdie tipe ossillasie nie 'n beduidende uitwerking op die akkuraatheid van 'n enkele skoot het nie. Maar met outomatiese opnames kan 'n interessante prentjie verskyn. Kom ons sê die vuurtempo is 1200 rds / min, d.w.s. tyd van een siklus - 0,05 sek. Met 'n eerste orde ossillasie tydperk van 0, 025 sek, het ons 'n veelvoudige frekwensie verhouding. En dit is 'n onontbeerlike voorwaarde vir resonansie met al die daaropvolgende gevolge - die wapen begin met so 'n krag skud dat dit uitmekaar kan val.
Kom ons gaan oor na ossillasies van die tweede orde (Fig. 2). Maar ek stel voor dat studente in geesteswetenskappe eers 'n eksperiment doen om die tekortkominge van opvoeding op die gebied van fisika uit te skakel. Jy moet 'n seuntjie neem (jy kan 'n meisie), hom op 'n swaai sit en swaai. Voor jou is 'n slinger. Staan langs die swaai en probeer om die seun met die bal te slaan. Na 'n reeks pogings kom u tot die gevolgtrekking dat die beste manier om te slaan is wanneer die teiken in die eerste fase van ossillasie is - die maksimum afwyking van die ewewigspunt. Op hierdie punt het die teiken nul spoed.
Kom ons kyk na die tweede orde diagram. Die tweede vibrasie knoop is ongeveer 0,22 van die einde van die loop geleë. Hierdie punt is 'n wet van die natuur; dit is onmoontlik om sulke trillings vir die draagbare balk te skep sodat die tweede knoop op die vrye punt val. Dit is waar dit is en hang nie af van die lengte van die vat nie.
Die ossillasie-amplitude vir die tweede-orde skema is laer, maar die ossillasietyd is reeds vergelykbaar met die tyd dat die koeël deur die boor gaan-0, 0025-0, 005 sek. Dit is dus reeds interessant vir enkelskiet. Stel u voor 'n vat van 1 meter lank om duidelik te maak waaroor ons praat. Die koeël beweeg binne 0, 001 sekondes deur die hele vat. As die ossillasieperiode 0,004 sekondes is, teen die tyd dat die koeël die loop verlaat, bereik die loop sy maksimum buiging in die eerste fase. Die vraag vir die geesteswetenskappe is: op watter punt (in watter fase) is dit die beste om 'n koeël uit die vat te skiet om konsekwentheid van die resultate te verseker? Onthou die swaai. By die nulpunt is die vektor van die stam se afbuigingsnelheid maksimum. Dit is moeiliker vir 'n koeël om hierdie punt op die vat te sny; dit het ook sy eie spoedfout. Dit wil sê, die beste oomblik vir die koeël om uit te vlieg, is wanneer die loop op die hoogste punt van die eerste afbuigingsfase is - soos in die figuur. Dan word onbeduidende afwykings in die koeëlsnelheid vergoed deur die langer tyd wat die vat in sy stabielste fase spandeer.
'N Grafiese voorstelling van hierdie verskynsel kan duidelik in die diagram gesien word (Fig. 4-5). Hier - Δt is die tydfout waarmee die koeël die snuit van die loop kruis. In fig. 4 is ideaal wanneer die gemiddelde opstarttyd vir koeëls saamval met die nulfase van die vat ossillasie. (Wiskundiges! Ek weet dat die snelheidsverspreiding nie-lineêr is.) Die gekleurde gebied is die verspreidingshoek van die bane.
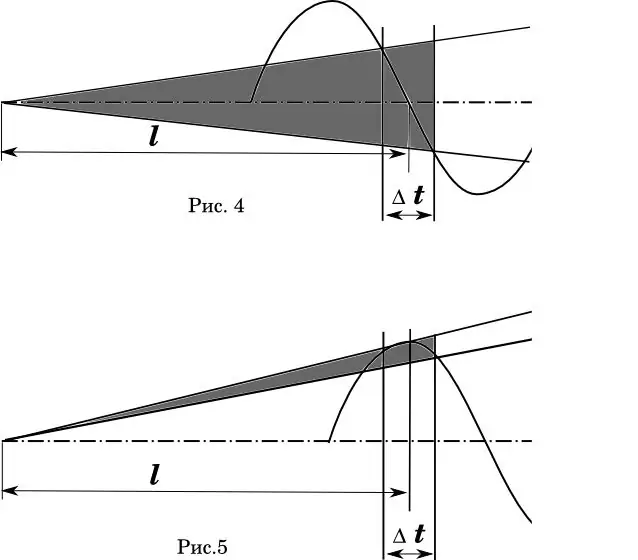
In figuur 5 bly die looplengte en snelheidsfout dieselfde. Maar die fase van die vatbuiging word verskuif sodat die gemiddelde vertrektyd saamval met die maksimum buiging van die loop. Is kommentaar oorbodig?
Is dit die kers werd? Hoe ernstig kan die afwykings wat veroorsaak word deur tweede-orde ossillasies, wees? Ernstig en baie ernstig. Volgens die Sowjet -professor Dmitry Aleksandrovich Ventzel, is die volgende resultate in een van die eksperimente verkry: die radius van die mediaanafwyking het met 40% toegeneem met 'n verandering in die vatlengte met slegs 100 mm. Ter vergelyking kan 'n vatverwerking van hoë gehalte die akkuraatheid met slegs 20%verbeter!
Kom ons kyk nou na die formule vir die trillingsfrekwensie:
waar:
k - koëffisiënt vir tweede -orde ossillasies - 4, 7;
L die looplengte is;
E is die elastisiteitsmodul;
Ek is die traagheidsmoment van die gedeelte;
m is die massa van die stam.
… en gaan voort met die analise en gevolgtrekkings.
Die voor die hand liggende gevolgtrekking uit figure 4-5 is 'n koeëlsnelheidsfout. Dit hang af van die kwaliteit van die poeier en die gewig en digtheid daarvan in die patroon. As hierdie fout ten minste 'n kwart van die siklustyd is, kan u alles opgee. Gelukkig het die wetenskap en die industrie baie goeie stabiliteit in hierdie saak bereik. En vir die meer gesofistikeerde (byvoorbeeld in die bankleuning) is daar alle voorwaardes vir die self-montering van patrone om die ontsnappingsfase van die koeël presies aan te pas by die looplengte.
Ons het dus 'n patroon met die laagste moontlike spoedvariasie. Die vatlengte is bereken op grond van die maksimum gewig daarvan. Die vraag na stabiliteit ontstaan. Ons kyk na die formule. Watter veranderlikes beïnvloed die verandering in die frekwensie van ossillasie? Vatlengte, elastisiteitsmodule en massa. Die vat word warm tydens die vuur. Kan die lengte van die vat hitte verander sodat die akkuraatheid beïnvloed word. Ja en nee. Ja, aangesien hierdie syfer binne honderdstes van 'n persent lê vir 'n temperatuur van 200 C. Nee, aangesien die verandering in die elastiese modulus van staal vir dieselfde temperatuur ongeveer 8-9%is, is dit by 600C byna twee keer. Dit wil sê, baie keer hoër! Die loop word sagter, die buigfase van die loop skuif vorentoe op die oomblik dat die koeël vertrek, daal die akkuraatheid. Wel, wat sê 'n deurdagte ontleder? Hy sal sê dat dit onmoontlik is om maksimum akkuraatheid op een vatlengte in koue en warm modus te kry! Die wapen het 'n beter prestasie met 'n koue of warm vat. Gevolglik word twee klasse wapens verkry. Die een is vir hinderlaagaksies, wanneer die doelwit vanaf die eerste - 'koue' skoot getref moet word, want die akkuraatheid van die tweede sal erger wees as gevolg van die onvermydelike verhitting van die vat. In so 'n wapen is daar geen dringende behoefte aan outomatisering nie. En die tweede klas is outomatiese gewere, waarvan die lengte van die loop aangepas is na die warm vat. In hierdie geval kan 'n moontlike mis as gevolg van die lae akkuraatheid van 'n koue skoot vergoed word deur 'n vinnige daaropvolgende warm en meer akkurate skoot.
EF Dragunov het die fisika van hierdie proses baie goed geken toe hy sy geweer ontwerp het. Ek stel voor dat u vertroud raak met die verhaal van sy seun Alexei. Maar eers sal iemand hul brein moet breek. Soos u weet, het twee monsters van Konstantinov en Dragunov die finale van die kompetisie genader vir 'n sluipskuttergeweer. Die ontwerpers was vriende en het mekaar in alles gehelp. Konstantinov se geweer is dus op 'koue modus' gestem, die geweer van Dragunov op 'warm'. Om die akkuraatheid van die mededinger se geweer te verbeter, vuur Dragunov sy geweer met lang pouses.

Kom ons kyk weer na die formule. Soos u kan sien, hang die frekwensie ook af van die massa van die vat. Die massa van die stam is konstant. Maar harde kontak met die voorkant lewer 'n onvoorspelbare positiewe terugvoer op die vat. Die stelsel-vat-voor-arm (steun) sal 'n ander traagheidsmoment hê ('n stel massas relatief tot die bevestigingspunt), wat beteken dat dit ook 'n faseverskuiwing kan veroorsaak. Dit is waarom atlete sagte ondersteuning gebruik. Dieselfde kenmerk word geassosieer met die toepassing van die beginsel van "hangvat", wanneer die voorkant van die wapen nie 'n harde kontak met die loop het nie en slegs daaraan vasgemaak is (die wapen) ontvanger, en die tweede kant raak óf glad nie die loop nie, óf raak deur 'n veerbelaste verbinding (SVD).
Laaste gedagte. Die feit dat dit met dieselfde vatlengte onmoontlik is om dieselfde akkuraatheid by verskillende temperature te verkry, gee 'n uitstekende rede om u brein te rek. Dit is slegs nodig om die lengte en / of massa van die vat te verander wanneer die temperatuur van die vat verander. Sonder om die lengte of die gewig van die vat te verander. Uit die oogpunt van die geesteswetenskappe is dit 'n paradoks. Uit die oogpunt van 'n tegnikus, 'n ideale taak. Die hele lewe van 'n ontwerper hou verband met die oplossing van sulke probleme. Die Sherlocks rus.






